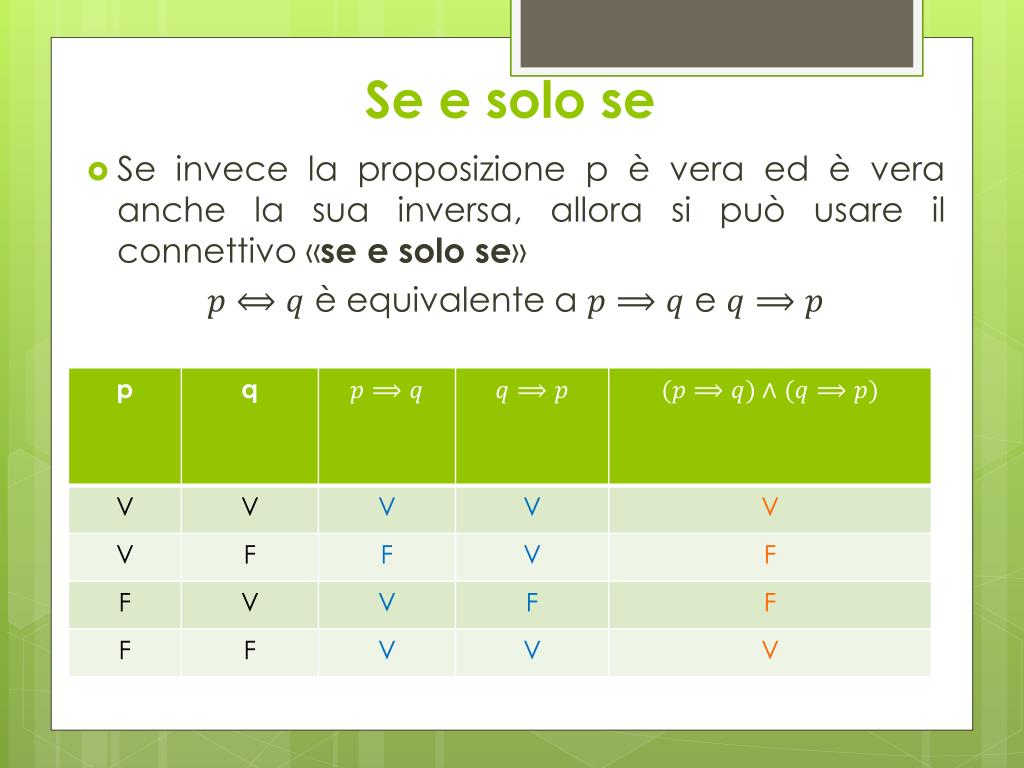
Nelle definizioni vale quando le due definizioni valgono contemporaneamente (es. un numero è pari <==> è divisibile per 2 l'interpretazione è se un numero è pari, allora è divisibile per due , se il numero è divisibile per due, allora è pari) per le dimostrazioni vale lo stesso ragionamento quando ti muovi da sinistra a destra per usare il se e solo se ti devi poter muovere anche da.. La frase "se e solo se" è usata abbastanza comunemente nella scrittura matematica da avere una propria abbreviazione. A volte il bicondizionale nell'affermazione della frase "se e solo se" viene abbreviato semplicemente in "se". Quindi l'affermazione "P se e solo se Q" diventa "P se Q". Citare questo articolo.

Piano inclinato esercizi con forza peso, forza elastica e forza di attrito radente YouTube
matematica.se
matematica.se

Matematica questões resolvidas i

Come usare la funzione PIÙ.SE di Excel Excel Academy

SÍMBOLOS MATEMÁTICOS Blog de matematicas, Simbolos matematicos, Matematicas

Se E Solo Se Simbolo poacobs
PPT Nozioni di logica matematica PowerPoint Presentation, free download ID2978130

Atividades Valor Posicional 3 Ano Yalearn Porn Sex Picture

Matematica questões resolvidas i

PPT Nozioni di logica matematica PowerPoint Presentation, free download ID2978130

Matematica questões resolvidas i

Come usare la funzione CONTA.SE di Excel Excel Academy

Matematica questões resolvidas i

06 LOGICA SE E SOLO SE DOPPIA IMPLICAZIONE E TAVOLA DI VERITA' VIDEORIPETIZIONE 06 YouTube

Se E Solo Se Simbolo poacobs

Tareitas SÍMBOLOS MATEMÁTICOS Simbolos matematicos, Cursos de matematicas, Matematicas

Matematica questões resolvidas i

40 frases de matemática que ressaltam a perfeição dessa ciência

Matematica questões resolvidas i
Se e solo se: condizione necessaria e sufficiente. Se e solo se è un'espressione utilizzata in logica e matematica per indicare una relazione di equivalenza tra due proposizioni. Questa relazione implica che le due proposizioni siano sia necessarie che sufficienti l'una per l'altra. In altre parole, una proposizione è vera se e solo se.. Condizione necessaria e sufficiente. Consideriamo due proposizioni A A e B B che soddisfano le seguenti condizioni: A A ). In questo caso diremo che A A è condizione necessaria e sufficiente per B B, e scriviamo A \Leftrightarrow B A ⇔ B. Spesso si dice anche: A A vale se e solo se vale anche B B, o più brevemente A A se e solo se B B.