Per ricavare queste regole andiamo semplicemente a moltiplicare i polinomi tra di loro. I principali prodotti notevoli che studiamo a scuola sono: Somma per differenza. Quadrato di binomio. Cubo di binomio. Potenza di un binomio. Quadrato di un trinomio. Potenza di un polinomio. Binomio per il falso quadrato.. Regola del quadrato di un binomio. Il quadrato di un binomio è uguale alla somma del quadrato del primo termine, più il doppio prodotto dei due termini, più il quadrato del secondo termine. In formule: \boxed { (a+b)^2 = a^2+2ab+b^2} (a +b)2 = a2 + 2ab+ b2. Per dimostrarlo, ci basta osservare che per le proprietà delle potenze:

11 quadrato di binomio YouTube

PPT IL CUBO DI UN BINOMIO PowerPoint Presentation, free download ID4029142

CL001 QUADRATO DI UN BINOMIO PARTE 1 YouTube
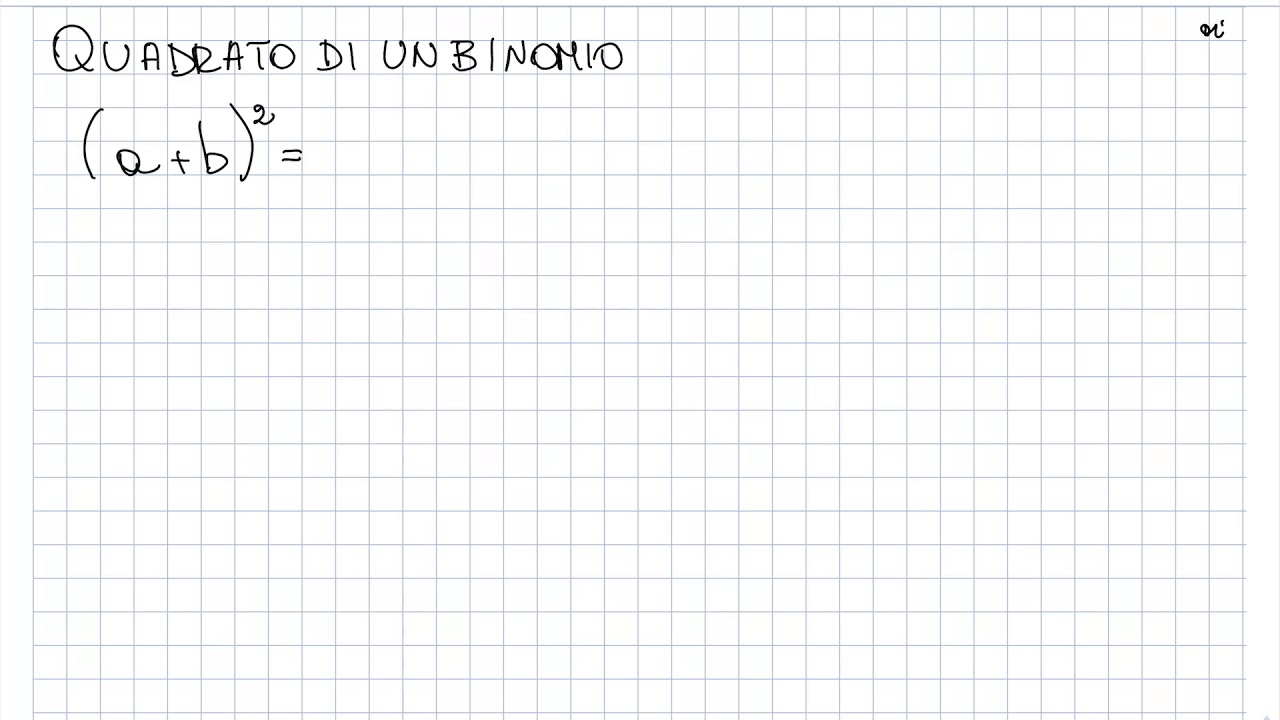
Quadrato di un binomio 1 YouTube

Interpretazione geometrica del Quadrato di binomio YouTube
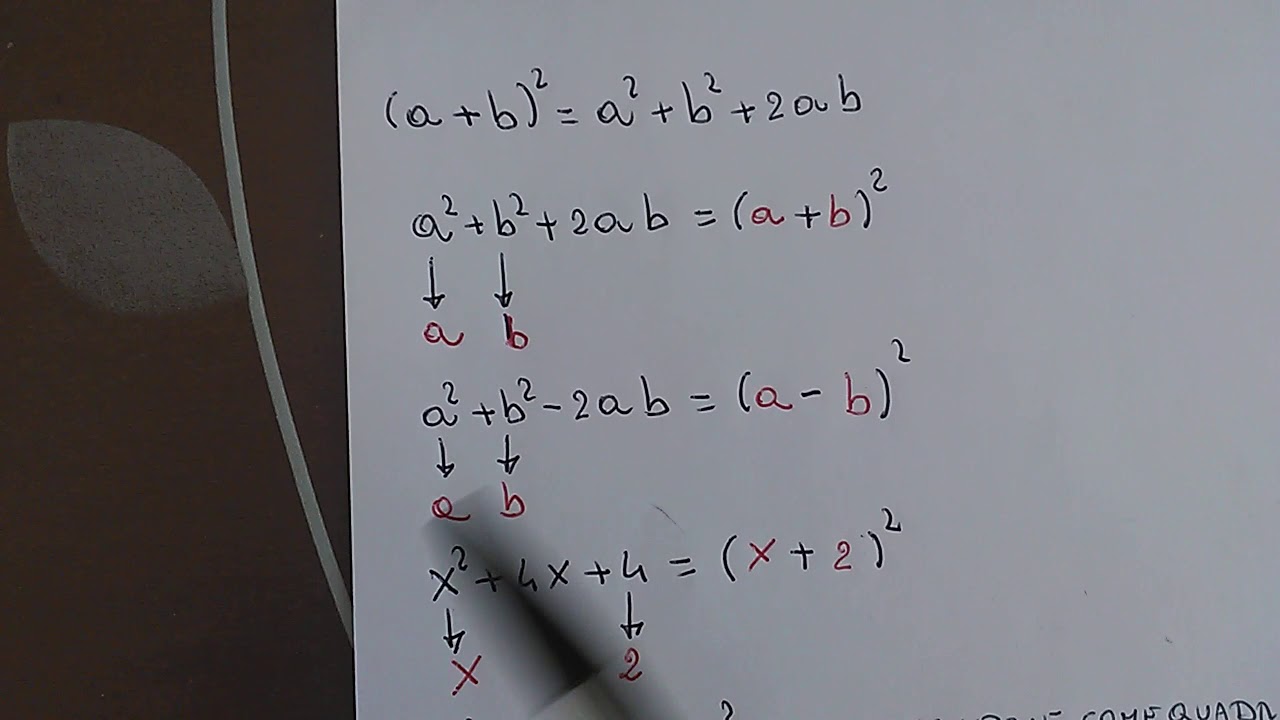
mediante quadrato di un binomio YouTube

Prodotti notevoli Quadrato di un binomio YouTube

Quadrato di binomio Andrea il Matematico

Quadrato di un binomio Math ShowMe

Ejemplo De Un Binomio

Quadrato di un binomio. Esempi YouTube

Quadrato di un binomio YouTube

Cubo Di Un Binomio Binomio al cubo YouTube Berardo Hatelme

Video quadrato binomio YouTube

Come si fa il quadrato di un binomio ilmessaggeero
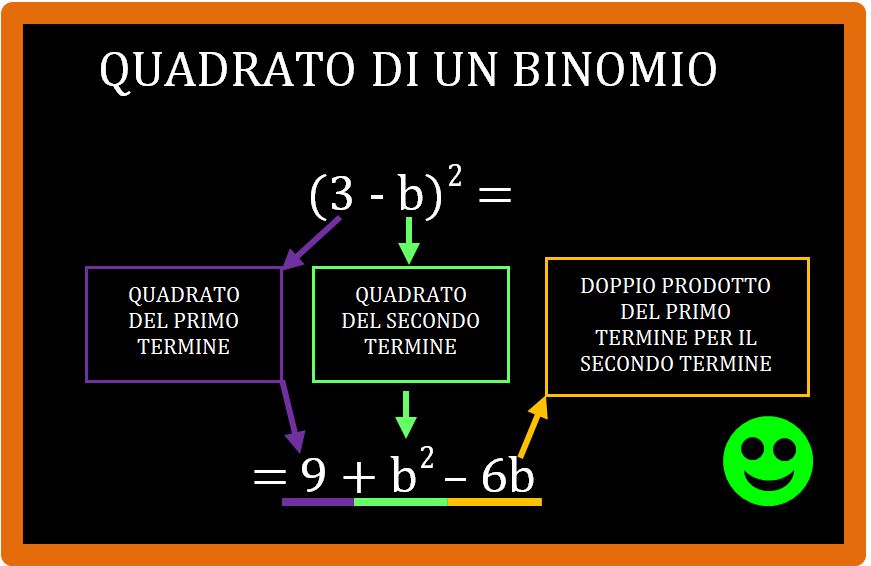
Altri esempi di quadrato di un binomio Matematica Facile
Altri esempi di quadrato di un binomio Matematica Facile

Il quadrato del binomio (con frazioni) secondo esercizio YouTube
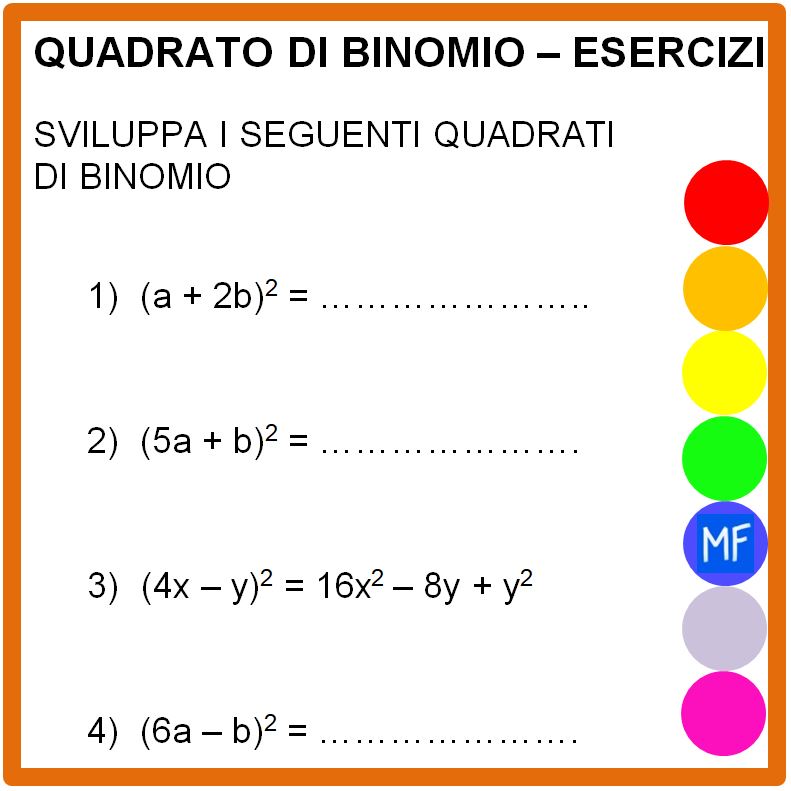
Altri esempi di quadrato di un binomio Matematica Facile

di polinomi quadrato di un binomio YouTube
Il trinomio di secondo grado viene talvolta detto falso quadrato perché, rispetto al quadrato di un binomio, il secondo termine manca del coefficiente e ha il segno opposto. Inoltre nell'insieme dei numeri reali tale trinomio non è mai fattorizzabile nel prodotto di due binomi.. Infatti il trinomo {x^2-3x+9} è il falso quadrato del binomio {x-3}. E' un falso quadrato, ricordiamo, poiché nei suoi termini compaiono sì i quadrati dei termini del binomio ma al posto del doppio prodotto abbiamo semplicemente il loro prodotto. Di conseguenza per il prodotto di partenza abbiamo: